Auto-Encoding Bayesian Inverse Games
Multi-modal distribution inference, uncertainty, generative modelling, differentiable programming
News
-
2024-09-10 We published the code for this work.
-
2024-08-17 This work was accepted to WAFR 2024. See you in Chicago!
About
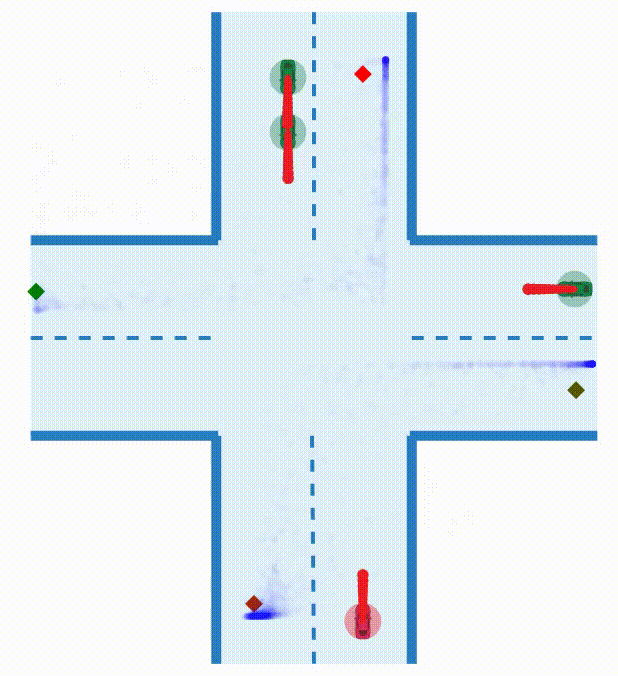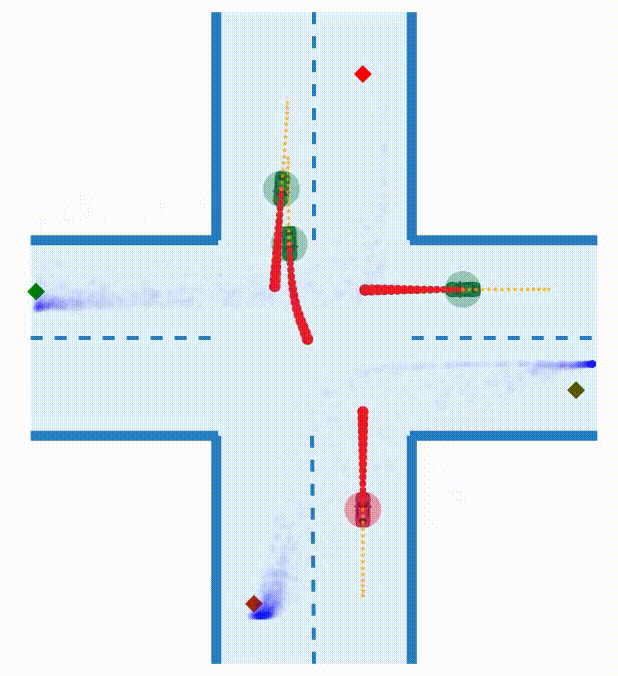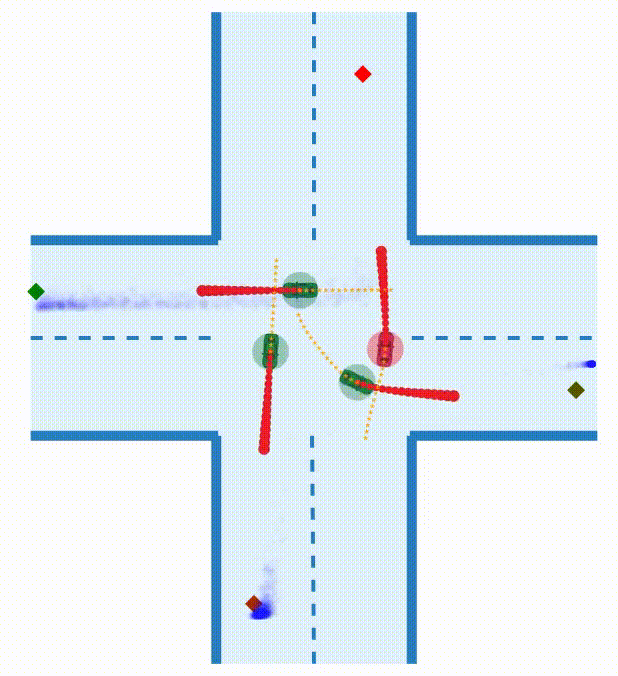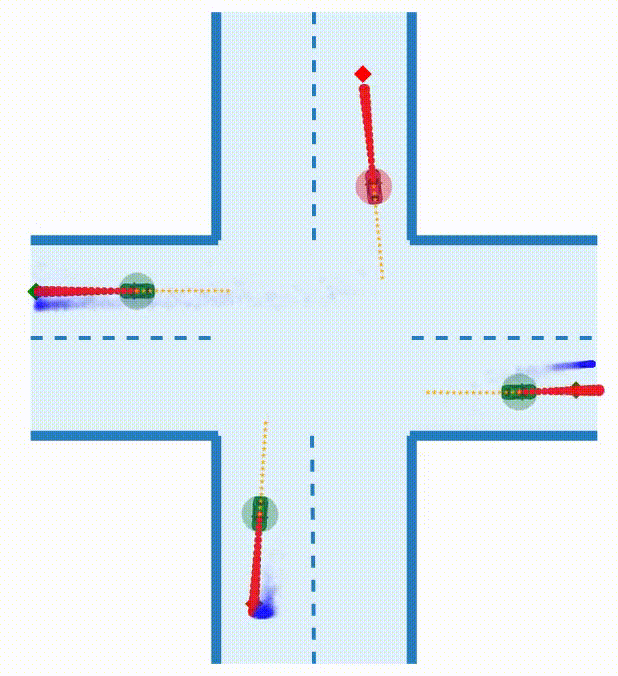
TL;DR: We propose a method for tractable inference of unknown parameters in noncooperative games by embedding a differentiable game solver into a variational autoencoder, and we assess this method in the context of interactive robot motion planning.
Abstract
When multiple agents interact in a common environment, each agent’s actions impact others’ future decisions, and noncooperative dynamic games naturally capture this coupling. In interactive motion planning, however, agents typically do not have access to a complete model of the game, e.g., due to unknown objectives of other players. Therefore, we consider the inverse game problem, in which some properties of the game are unknown a priori and must be inferred from observations. Existing maximum likelihood estimation (MLE) approaches to solve inverse games provide only point estimates of unknown parameters without quantifying uncertainty, and perform poorly when many parameter values explain the observed behavior. To address these limitations, we take a Bayesian perspective and construct posterior distributions of game parameters. To render inference tractable, we employ a variational autoencoder (VAE) with an embedded differentiable game solver. This structured VAE can be trained from an unlabeled dataset of observed interactions, naturally handles continuous, multi-modal distributions, and supports efficient sampling from the inferred posteriors without computing game solutions at runtime. Extensive evaluations in simulated driving scenarios demonstrate that the proposed approach successfully learns the prior and posterior objective distributions, provides more accurate objective estimates than MLE baselines, and facilitates safer and more efficient game-theoretic motion planning.